5850. Mathematical platforms

In older games, which have 2D graphics, one can run into the next situation. The hero jumps along the platforms or islands that hang in the air. He must move himself from one side of the screen to the other. The hero can jump from any platform number i to any platform number k, spending (i – k)² * (y_i – y_k)² energy, where y_i and y_k are the heights where these platforms hang. Obviously energy should be spent frugally.

You are given the heights of the platforms in order from the left side to the right. Can you find the minimum amount of energy to get from the 1-st (start) platform to the n-th (last)?

Input. The first line contains the number of platforms n (1 ≤ n ≤ 4000). The second line gives n integers – the heights of the platforms, which absolute values are not greater than 200000.

Output. Print the singe integer which is the minimum amount of energy to get from the 1-st platform to the n-th.

Sample input	Sample output
4 1 2 3 30	731

SOLUTION

graphs – Dijkstra algorithm

Algorithm analysis

Consider each platform as a vertex of the graph. Between each pair of vertices i and j make an undirected edge g[i][j] with weight (i – j)² * (y_i – y_j)² (the amount of energy required to move between vertices i and j). Now you must find the minimum path between the first and the last vertices, that can be done using Dijkstra’s algorithm.

There is no need to keep the graph in memory, since all values of g[i][j] can be calculated using the above formula.

Example

Graph and its weight matrix are given below:

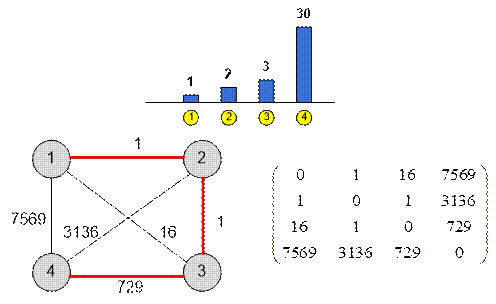
The hero should move along the platforms in the order 1 → 2 → 3 → 4, spending for it 1 + 1 + 729 = 731 energy units.

Algorithm implementation

Declare the constants:

· MAX – the number of platforms;

· INF – thr maximum number of type kong long;

#define MAX 4001

#define INF 0x3F3F3F3F3F3F3F3FLL

Declare the arrays:

int used[MAX];

long long m[MAX], dist[MAX];

Read the input data – the platform heights. Platforms are numbered from 0 to n – 1.

scanf("%d", &n);

for (i = 0; i < n; i++)

scanf("%lld", &m[i]);

Initialize the array of shortest distances dist.

memset(dist, 0x3F, sizeof(dist));

dist[0] = 0;

Run the Dijkstra’s algorithm from the vertex 0.

for (i = 1; i < n; i++)

{

min = INF; w = -1;

for (j = 0; j < n; j++)

if (!used[j] && dist[j] < min) { min = dist[j]; w = j; }

if (w < 0) break;

for (j = 0; j < n; j++)

{

Compue the distance len between the vertices w and j.

long long len = (w - j) * (w - j) * (m[j] - m[w]) * (m[j] - m[w]);

If the shortest distance to the vertex j has not yet been calculated, then relax the edge (w, j).

if (!used[j] && dist[j] > dist[w] + len) dist[j] = dist[w] + len;

}

used[w] = 1;

}

Print the shortest distance to the vertex n – 1.

printf("%lld\n", dist[n - 1]);

Java implementation

printf("%lld\n", dist[n - 1]);

import java.util.*;

public class Main

{

static int used[];

static long m[], dist[];

static long INF = 1000000000000000000L;

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

m = new long[n];

for (int i = 0; i < n; i++)

m[i] = con.nextLong();

used = new int[n];

dist = new long[n];

Arrays.fill(dist, INF);

dist[0] = 0;

for (int i = 1; i < n; i++)

{

long min = INF;

int w = -1;

for (int j = 0; j < n; j++)

if (used[j] == 0 && dist[j] < min) { min = dist[j]; w = j; }

if (w < 0) break;

for (int j = 0; j < n; j++)

{

long len = (w - j) * (w - j) * (m[j] - m[w]) * (m[j] - m[w]);

if (used[j] == 0 && dist[j] > dist[w] + len)

dist[j] = dist[w] + len;

}

used[w] = 1;

}

System.out.println(dist[n-1]);

con.close();

}

}